目次
数学史 黎明期
数学史 黎明期に追加したい内容
- 演算記号の歴史
- フランスの20進数
- 古代ローマの数学
- 古代日本の数学
- 円周率
- 分数、小数点の表記
- 古代ギリシアの論理思考
- 紙の歴史 製紙は最初は布だった
- 中国は先進国 衰退していった。
歴史区分
今回の数学史の説明は、ヨーロッパ史の歴史区分でいうと古代~中世となります。
| 区分 | 年代 | 内容 |
|---|---|---|
| 原始 | 先史時代 | 人類の誕生以降 |
| 古代 | ~5世紀 | 文明の発生以降 |
| 中世 | 5~14世紀 | 封建制度以降 |
| 近世 | 15~17世紀 | ルネサンス以降 |
| 近代 | 17~19世紀 | 産業革命以降 |
| 現代 | 20~21世紀 | 第二次世界大戦以降 |
科学史家の伊東 俊太郎氏によれば、人類史は「人類革命、農業革命、都市革命、精神革命、科学革命、環境革命」の6つに分けることができる。
| 革命 | 内容 |
|---|---|
| 人類革命 | 人類の誕生 |
| 農業革命 | 農耕の始まり、定住、文化の誕生 |
| 都市革命 | 分業・社会階層、文明の誕生 |
| 精神革命 | 世界宗教、哲学の始まり |
| 科学革命 | 近代科学の成立、産業革命 |
| 環境革命 | 自然との共生 |
文明の誕生
狩猟・採集では人は移動しながら生活していましたが、農耕・牧畜を覚えることで定住化が進みました。
畑をたがやして種を蒔いてある程度ほったらかすことで暇な時間もでき、刈り取りの道具や刈り取りを運ぶ道具、調理するための土器を作られるようになりました。
やがて一定の地域に少しずつ定住する者が増えて集団ができます。
しかし、集団から村や町や都市になるには段階が必要でした。
- 天水農業で雨だけに頼る方法はあまりに不安定で、土地が弱る(土の微生物がいなくなる)と移動をしなければならなかった。
- 川の適度な氾濫が起こることにより、肥沃(ひよく:地味が肥え、作物がよくできること)な土地が生まれ、土地が痩せることが無いから移動をしなくても良くなった。
- 灌漑農業という川から水を引いて溜池を作るなどの方法が生まれることで安定した食料の確保ができるようになった。
これらにより都市国家となって発展していきました。
人が定住し文明が発達し、集団で生活を始めると必ず権力者が生まれ、やがて支配階級が出来上がります。
農業でたくさん野菜や果物が収穫できるようになったので、農業に従事しない神官、商人、職人、戦士など農民以外の職業も生まれてきました。
神官たちは暦作成のために天文観測をし、それにより占星術も生まれました。
土地の区画などで測量技術や作図技術が発達し、税(収穫した穀物)を取り立てるのに算数(計算や比率の考え等)が発達した。
古代文明
大きな川があるところに文明ができる。エジプトはナイル川、メソポタミアはチグリス川とユーフラテス川など。
今は世界四大文明とは言わないようだ。
<html>
<img src=“http://www12.plala.or.jp/rekisi/image459.jpg”>
</html>
数学の語源
数学(mathmatics)の語源
「数学」は中国伝来の言葉、ヨーロッパでの語源はギリシア語の「学ぶことができるもの」を意味する「マテーマタ(mathema)」
幾何学の語源
幾何学の英語は「geometry」 “geo”:土地、“metry”:測量 日本は中国語の「幾何 (キーホ) 」を輸入し「キカ」に。 geo(ジーホ)→キーホという音訳した説があるが、音訳は間違い(数学的対象の量一般を意味)の論文がある。
日本は江戸時代初期平安時代までハ行がなかった。
数を知る
古代の人々は、1、2、たくさん や 1、2、3、たくさんなど3または4以上を数える術すべを持たず、【たくさん】と表現しました。
それでも「無」の概念は使っていました。狩猟をしてて何も取れなかったら、何も無いですからね。
現在でもパプアニューギニアやオーストラリアの原住民の中には、物を数える時に「1、2、たくさん」と数える種族がいるそうです。
ちなみに動物や昆虫は生まれながらにして数を数える能力がある。ただ数を数える数に限界がある。頭がいいと言われるカラスが数えられる数も4から5、訓練によって7つまで数えられるようになったという報告もあります。
数の概念
イギリスの数理哲学者ラッセルが「2日の2と2匹のキジの2が同じ2であることに気付くまでには限りない年月が必要だった」と言っている。
現代の人間の子どもも数の概念をあらかじめ身につけているわけではないし、1から100までの数字を言える子どもが100個のものを数えられるわけではない。
下記項目が分かって、初めて数の概念を理解していることになる。
- 数を唱える、数の順序を知る(1,2,3,4,5,6,7,8、…)
- 数の集合を知る(0,3の固まり、5の固まり)
- 数の対応(1対1)…(スプーンとお皿、コップとストローなど)
- 数の比較(同数発見)…形や色、位置が変わっても、数はかわらない。
- 数の分割…オハジキを分割しても合併させても、総数は変わらない。→ 6歳頃から理解できる。
1対1対応
「calculate」は「計算する」の意味の他に、calc「石」-ate「〜する」で「石で数える」という意味もあります。
何か物を「1,2,3…」と数えることは、ものと数字を1対1に対応させる作業です。
数を使えなかった時代の人々が、手や体の部位や小石で数えたいものを1対1対応させていた。
例えば農家が30頭の羊を飼っていたとします、この農家の人は「30」という数は使えませんが、1対1対応を使って「数える」ことは知っています。
朝に放した羊が全部戻ったかどうかを確認するには、袋の中に多数の小石を入れて持って行き羊を1頭放す毎に小石を袋から出して岩の上にでも並べて置きます。
そして夕方、羊が1頭戻って来る毎にその小石を袋に戻します。岩の上の小石がなくなれば、羊が全部戻ったことになります。
「5歳8ヵ月」の子どもに「同じ数のいくつかの花ビンと花」を与えて、花ビンの1つ1つに花を1本ずつ入れてから花を取って束ねた後に「花ビンと花は、どちらが多いか?」と質問すると、「花ビンが多かった」と答える。これは花を束ねたので「少なく見えた」からである。
http://shisly.cocolog-nifty.com/blog/2015/08/post-f70c.html
http://www.nihongo.com/aaa/chigaku/suugaku/kigu.html
http://suikukai.com/category/1782348.html
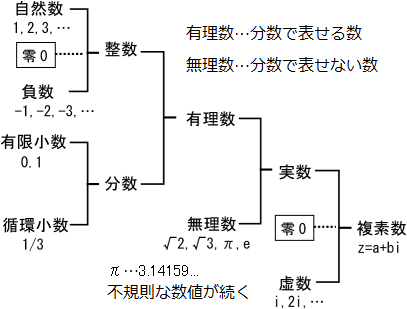
数の分類
位取り記数法
定めた値を一区切りと考えて、そこから先は定めた値を組合せて数えていくことです。N 進法ともいいます。
10進法
人が日常使用している数値は10進法です。例えば30は10を3つと考えます。
10進法は、人の10本の指に由来します。
ちなみに、豊臣秀吉は多指症で指が6本(右手に親指が2本)あり信長から「六ツめ」と異名されていたそうです。
12進法
10進法と並んで多くの文明で使われてきたのが、12進法の考えである。
現在も12進法は、時計の目盛りは12時間、1ダースは12個などに使われている。
何故かというと約数が多いからである。
10の約数は1,2,5,10の4種類
12の約数は1,2,3,4,6,12の6種類
数えることが主流な文化では10進法を用いたのに対して、分けることが主流な文化では12進法を用いた。
天文学が発達した文明では方角を分ける際に、12という数が都合が良かった。
60進法
時計は1分60秒で60進法になっている。
約数の多い12でも分けられない数が5である。
5でも分けられる数を考えた時に、12×5=60だった。他にも10と12の最小公倍数で60。
また、紐を使ってコンパスのように円周を六等分する方法を知っていたから60進法を使うようになったのかも知れない。
数学をつかった裏技?!ピザを六等分しよう①
60は、1,2,3,4,5,6で分けれるし、10でも12でも15でも分けられる数である。
60の約数は1,2,3,4,5,6,10,12,15,20,30,60の12種類
メソポタミア文明時代(バビロニア数字)では60進法が使われていた。
古代バビロニアでは、1年を360日と考えていたので全円周を1年にたとえて360度とし、六等分した60を大切な数と考えて60進法とした。
<html> <img src=“https://upload.wikimedia.org/wikipedia/commons/1/16/Babylonian_numerals.jpg” style=“zoom:0.7;”> </html>
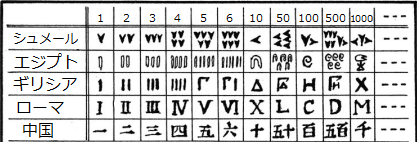
桁記号記数法
桁記号記数法とは、ある大きさの値になると別の記号を使う方法です。
だいたい、10、100、1000と位が上がることに新しい使います。
13と24と3888をローマ数字で数を表してみます。
13 = 10 x 1 + 1 x 3
= X + III
= XIII
24 = 10 x 2 + (−1 + 5)
= XX + IV
= XXIV
3888 = 1000 x 3 + 500 + 100 x 3 + 50 + 10 x 3 + 5 + 1 x 3
= MMM + D + CCC + L + XXX + V + III
= MMMDCCCLXXXVIII
ローマ数字の4(IV)や9(IX)と表現して4(IIII)や9(VIIII)としないのは、ローマ数字では4つ以上記号を並べないというルールがあるからです。
他の記号でも4つ以上並ぶようなら、(−1 + 次の位の記号)のようにします。
49 = (-10 + 50) + (−1 + 10) = XL + IX = XLIX
計算器具
足し算で先程の 13 + 24 = 37をローマ数字で数を表してみます。
XIII + XXIV ------- XXXVII
このように桁記号記数法では計算が大変なため、「アバカス」という計算器具が使われていました。
木・石・金属などでできた板に溝を彫り、その溝の上で豆や小石を動かして計算を行います。
後に中国伝わり珠を串刺した形式で10進法と16進法の計算が可能であったが、17世紀に中国の明から日本に伝わり10進法専用になり現在の「そろばん」となります。
中国ではそれまで「ぜい竹」という細い竹の棒を使用していましたが、今では占い師しか使わなくなりました。
<html> <img src=“https://upload.wikimedia.org/wikipedia/commons/b/b5/RomanAbacusRecon.jpg”> <img src=“https://upload.wikimedia.org/wikipedia/commons/3/35/Science_museum_030.jpg” style=“zoom:0.15;”> </html>
アラビア数字
現在、一般に使われているのはアラビア数字(インド数字)です。
本当はインド数字なのですが、8世紀にインドの隣にあるアラビアに伝わり13世紀以降にイタリアからヨーロッパに広がったことからアラビア数字と呼ばれるようになります。
伝来の歴史は後で説明します。
ちなみに、インドでは板の上に砂をまいて、そこで計算していたため歴史的な記録が残らなかったのです。
特徴
ゼロの発明
インドでは、ゼロの発明したとよく聞くが何のことなのか。
ゼロには3つの使い方があります。
- 記号(空位)としてのゼロ
- 数(演算の対象)としてのゼロ
- 原点としてのゼロ
記号(空位)としてのゼロ
ただ何もないということの記号であれば、古代バビロニア時代(60進法)にもありました。
例えば、アラビア数字のゼロ「0」を位の位置を表わした場合、一番右の数字は1の位、右から2番目の数字は10の位、右から3番目の数字は100の位というルールになっています。。
例えば「307」は、1の位が7、10の位が空位、100の位が3であることを表してします。
古代インドでもゼロは空白で表していたが、下記のようにすると見た目の表現的にも位の位置の区別が難しかったので、「0」を記号として使うようになったと思われます。
2 3 … (203) 2 3 … (2003)
「0」という記号が使われたもっとも古い記録は西暦686年のカンボジアに残っていて、少なくてもインドでは6世紀には「0」が一般に広く使われていたと推定されています。
数(演算の対象)としてのゼロ
古代エジプト辺りでは「図形の数学」として、「数」と「形」がセットで発達してきた 。 図形的に「0」は長さも面積もなく図形の世界には登場しない。意味をもたないと嫌われていた(宗教的にも) がインドでは「図形の数学」もそれほど発展せず、「数」が「形」に縛られる必要はなかった結果、インドのほうが数としての「0」の使用が進み、ヨーロッパはそれを取り入れる形になった。
17世紀の数学者パスカルでさえ、「0から4を引いても0だ」と言っていた。
日本も江戸時代末の1830年に刊行された「算法新書」から。
キリスト教(ギリシアを中心とした西洋)は神以外の無限を嫌ってゼロを否定し、仏教(インド)はゼロを空の概念から止揚した。
原点としてのゼロ
インドでは負債をあらわすときに負の数を使用していた。
ヨーロッパへはゼロの概念とともにアラビア経由で伝えられたが、ゼロの演算と同じく受け入れられるには時間がかかった。
負の数は-3個のリンゴのように「個数」ではイメージしずらい。
負の数は「数値線」があればイメージしやすい。
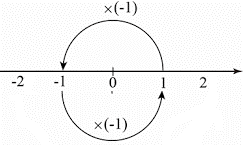
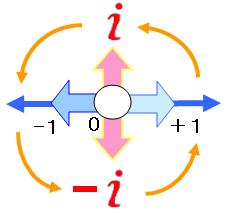
負数は小学校では教えない。虚数は高校から
虚数とは何か?複素数とは何か?が一気に分かりやすくなる記事
天文学
暦(太陰暦)
メソポタミア文明シュメール人が考案。太陰暦は「月」が基準
- 最初は遊牧民は家畜の餌となる草が生える時期を知るため
- 農耕が始まるとタネまきの時期を正確に知るため
- 暦を知るため 月の公転周期により、1月30日で年12ヶ月で1年360日とした。
本当の周期は約29.5日、1月を29日と30日で調整(354日)
後に暦と季節のずれより太陽暦の要素を入れ太陰太陰暦に。
七曜制は月の変化(新月~上弦~満月~下弦~新月)の間隔が、それぞれ約7日のため、「7日」を一まとめしたのが由来。
月曜日の「Monday」は月(Moon)からきている。
暦(太陽暦)
エジプトではナイル川の定期的な氾濫により測量技術が発達。
1年が365日でめぐることを知り、季節の変化と一致しない太陰暦から地球が太陽の周りを回る周期が基の太陽暦に移行。
初めは1月は30日で年12ヶ月、5日の祝日を入れて365日とする民衆暦を工夫し、後に4年に1度の閏年をいれるようになった。
農作物の栽培に適合しているために次第に広く使われるようになり、カエサルがこれをローマに導入してユリウス暦とし、地中海世界・ヨーロッパで広く行われるようになった。
古代バビロニアの数学
古代バビロニアは、メソポタミア文明は含まれる。
メソポタミアは北と南と分かれるが、南側はウバイド期→ウルク期→バビロニア期となっており、ウルク期はシュメール人が文化の担い手だった。
シュメール人が都市、法典、楔形文字(くさびがたもじ)、青銅器、太陰暦や太陰太陽暦、七曜制、60進法も生み出し、エジプト文明、インダス文明の誕生にも影響をあたえた。
数学としては、粘土板に正方形の長さの1辺の長さを30とした時の対角線の長さが60進法で刻まれており、その値はルート2の1.41421・・・で小数点以下5桁まで現在の値と一致していた。
古代エジプトの数学
古代エジプト史は大きく3つの時代に分けられます。
- 古王国(紀元前2700~紀元前2200年頃)
- 中王国(紀元前2100~紀元前1700年頃)
- 新王国(紀元前1600~紀元前1100年頃)
古王国はすべてのピラミッド(クフ王が有名)が造られた時代。
エジプトが1日を24時間にした。エジプトは10進法で、はじめは昼と夜をそれぞれ10に分けて20としたが、昼と夜の境界の時間をそれぞれに付け加えて24としたそうです。
数学は、灌漑や干拓のための測量、課税のための人口調査、生産物の貯蔵と配分、暦学、ピラミッドをはじめとする建設など「実用的な数学」として活用された。
幾何学では、円の面積の近似値、角錐台の体積を求める公式、半球の表面積を求める方式などの業績を残した。
記号代数学は存在しなかったが、言語による修辞的な代数によって単独方程式や連立方程式を解いた。等差級数や等比級数にも関心を示した。
かけ算は「たし算」と「2倍」のみを組み合わせて計算。
分数は2分の1や3分の1など分子が1と例外的に3分の2を使用。
古代ギリシャの数学
エジプトの測量や作図の技術は高度に発達していたが、なぜそれが正しいのか誰も証明していなかった。
若い頃にバビロニアで天文学とエジプトで測量や作図を学んだタレスが証明して図形に「論理」を持ち込んで幾何学という学問にまで高め人々に広めた。(論証幾何学)
論理的思考が出来たのは、当時のギリシア社会の民主制が関係していると思われる。
タレスの論証幾何学は、その後、ピタゴラスやユークリッドに受け継がれ、数学の発展に大いに貢献していくことになります。
タレス(BC.624-BC.546頃)
ギリシアの植民地イオニアのミトレス出身。
若い頃にサモス島で商業を営み、商用で西アジアやエジプトなどを往来して、天文学や測量や作図などの知識を持ち帰った。
世界を構成する物は「神」が作ったものだという「神話的思考」から脱却し、ある事象を観察し自然法則を導くという「自然科学的方法」を初めて体現した。天文学では初めて日食を予言。
ピラミッドの影の長さからピラミッドの高さを求める方法を考案。
「万物は水なり」の名言を残す。
ピタゴラス(BC.572-BC.492頃)
サモス島出身。タレスの弟子のアナクシマンドロスに学ぶ。世界最初の音楽理論を考案。幾何学だけではなく数論もやり、偶数や奇数や素数、約数、倍数などいろんな数に名前をつけた。
三平方の定理($a^2 + b^2 = C^2$)が有名。
イタリアのクロトンで宗教・哲学・政治を学ぶ一種の宗教集団を開き、何百人の弟子と生活した。弟子の研究でも教王のピタゴラスの名前で発表した。ピタゴラスの教義は「万物は数なり」。
やがて国の政治まで手をだし、反感をかって追放された。
プラトン(BC.427-BC.347)
今の大学の起源であるアカデミアの創設者。ソクラテスの教えやピタゴラス学派の数学にひかれ、哲学・数学を研究した。
アリストテレス(BC.384-BC.322)
プラトンのアカデミアで学び、ピタゴラス学派の数の理論を研究し、より理論的・実証的に学問を目指した。
アリストテレスはアレキサンドロス大王(アレクサンダー大王、アレクサンドロス3世)が13歳の時に家庭教師に付いています。
古代言語研究の第一人者、フレデリック・ジョージ・ケニオンの『古代の書物』によれば、このアリストテレスこそが本を体系立てて活用した蔵書家の始祖であり、「アリストテレースと共にギリシア世界は口頭の教えより読書の習慣へと移った」と記されています。
アレキサンドロス大王の大遠征
アレキサンドロス大王(アレクサンダー大王、アレクサンドロス3世)によって文明が発展した部分があるので時系列を追ってみます。
アレキサンドロス大王の父親なのでギリシア北部のマケドニア王国でフィリッポス2世です。
マケドニア王国は、アテネなどから見るとあくまでも辺境の地。同じギリシャ人ながら、粗野で文化が遅れていると馬鹿にされていました。しかしフィリッポス2世が23歳で即位すると、財政の整備、軍政改革を行い瞬く間に国力をつけます。そして、前357年よりギリシャの各ポリスに侵攻を開始。その勢いはとどまるところを知らず、前338年、カイロネイアの戦いでギリシャ連合軍と戦いこれに圧倒的な勝利を収めます。しかし、フィリッポス2世は前336年に暗殺されてしまいます。そこで即位したのは20歳のアレクサンドロス3世、通称アレクサンダー大王(前356~前323年、位前336~前323年)です。アラビア語やペルシア語ではイスカンダルと呼ばれている。
アレクサンドロスは前332年にはエジプトにも遠征し占領します。そして、ナイル川の河口ににアレクサンドリアという大都市を建設します(アレクサンダーの名にちなむ。なお、同種の街は各地に作られたが、その中でもエジプトのアレクサンドリアが発展した)。
| 名前 | 開始年 | 終了年 | 年齢 |
|---|---|---|---|
| ペロポネソス戦争 | BC431 | BC404 | (75) |
| フィリッポス2世、マケドニア王として即位 | BC359 | (3) | |
| アレクサンドロス3世、誕生 | BC356 | 0 | |
| アリストテレス、アレクサンドロス3世の家庭教師として招かれる | BC343 | BC340 | 13 |
| カイロネイアの戦い | BC338 | 18 | |
| コリント同盟(ヘラス同盟)、成立 | BC337 | 19 | |
| マケドニア王フィリッポス2世が暗殺される | BC336 | 20 | |
| アレクサンドロスの東方遠征はじまる | BC334 | BC324 | 22 |
| グラニコス川の戦い | BC334 | 22 | |
| イッソスの戦い | BC333 | 23 | |
| ティルス大攻城戦 | BC332 | 24 | |
| アルベラ(ガウガメラ)の戦い | BC331 | 25 | |
| アレクサンドロス、アケメネス朝ペルシアを滅ぼす | BC330 | 26 | |
| ヤクサルテス川の戦い | BC329 | 27 | |
| ヒュダスペス河畔の戦い | BC326 | 30 | |
| マッロイ戦役 | BC326 | BC325 | 30 |
| アレクサンドロスは若くして病死 | BC323 | 32 |
ユークリッド(エウクレイデス) (BC.330-BC.275頃)
ユークリッド幾何学の創始者。複数人の共著の一人の説とも。
ユークリッドは、アテネにあるプラトンの創設した研究教育機関アカデミーに学び、エジプトのプトレマイオス1世に招聘されてアレクサンドリアにある大図書館兼研究所「ムゼイオン」で数学部門の長を務め、数学の発展に大きな足跡を残した。
13巻からなる数学書「原論」を著わす。エジプトのアレキサンドリア大学校で講義するときの教科書であった。
幾何学以外にピタゴラスらの数論も全体の三分の一くらいある。
プトレマイオスは国王ピリッポス2世が息子アレクサンドロス(アレキサンダー大王)のために哲学者アリストテレスを招いて作ったミエザの学園に学んだ「学友」でもあった。。
ユークリッド原論
| 第1巻 | 定義からピタゴラスの定理まで |
|---|---|
| 第2巻 | 幾何学的代数(2 次方程式の解法など) |
| 第3巻 | 円論 |
| 第4巻 | 内接円,外接円,正多角形 |
| 第5巻 | 比の理論 |
| 第6巻 | 相似形 |
| 第7~9巻 | 数論(互除法など) |
| 第10巻 | 平方根 |
| 第11~12巻 | 立体幾何 |
| 第13巻 | 正多面体 |
ユークリッド原論は当時の数学的知識を体系的にまとめたものです。他の文明における数学的記述が「問題と解法」という観点から書かれていたのに対し、「定義・公理から定理へ」という形式は現代の学術書にも通じるものです。まさに、世界最古の学術書といえます。
しかし、その内容には問題点もいくつかあります。一部の定義に見られる曖昧さ、明示されない議論の前提(公理)の存在、そして第5公準(平行線の公理)です。これらの問題点が解決するのは19世紀に入ってからです。問題点の存在は原論の意義を低めるものではありません.
- ニュートンは著書「プリンキピア」を原論の体裁にしたがって著述した
- 19世紀になってもイギリスの一部の学校では教科書として使われていた
- 歴史上聖書の次に読まれた本と言われている
アルキメデス(BC.287-BC.212頃)
円周率を3.14とし、小数点以下2桁まで正確に求めた。
アルキメデスの原理として有名な「浮力の法則」や「てこの原理」など数々の業績を残した。
デオファントス(200-214 - 284-298頃)
エジプトのアレクサンドリアに住んでいた代数学の父。
ディオファントスは著書の「算術(Arithmetica)」において、既に知られている問題をまとめ、更に自分でも新しい問題を作りました。
エジプトの都市アレクアンドリアの図書館に納められていましたが、度重なる侵略や反乱で図書館は燃え、算術全13巻のうち6巻分は失われずに残りました。
この算術はラテン語に翻訳され1621年にヨーロッパで出版されました。それを熱心に読んでいたのがフランスの数学者ピエール・ド・フェルマーでフェルマーの最終定理をメモとして残すことになります。
中国の数学
中国では漢(紀元前1世紀ごろ)時代に編集された官吏のための教科書「九章算術」がほぼ完全な形で残っている。また、これより古い「算数書」が1983 年に前漢の墓から発見された。
九章算術
9章に分かれ、延べ246個の問題を収めた、問題集形式の数学書である。理由を説明することはめったにしなった。
あくまで実用面でしかなく数学は独立した学問とはみなされず、新しく定理や法則を作ると言う伝統が無かった。
| 一章 | 方田 | 田の面積の計算 分数計算 |
|---|---|---|
| 二章 | 粟米 | 異なる交換比率の商品を交換するための比例計算 |
| 三章 | 衰分 | 商品とお金との分配や比例計算 利息計算 |
| 四章 | 少広 | 正方形や立方体の一辺(平方根や立方根) πの近似値 |
| 五章 | 商巧 | 土木工事に伴う体積計算 |
| 六章 | 均輸 | 租税の計算 複雑な比例計算 |
| 七章 | 盈不足 | 物の分配に関する整数論的問題 |
| 八章 | 方程 | 連立1次方程式 |
| 九章 | 句股 | ピタゴラスの定理とその応用 簡単な2次方程式の解法 |
九章算術は問題を出し解法と答えを出す帰納的な手法(具体的な事柄から一般的な事柄へと遡る考え方)である。具体的には問題の記述の後、「答曰く、」ではじまる答えと、「術曰く、」ではじまる解法の記述という具合である。
演繹的な手法(一般的な事柄から他の具体的な事柄へと押しひろめる)のヨーロッパ・アラブ数学とは異なり、中国の以後の数学書はこの記述方法を採った。
このスタイルは日本にも輸入され、和算の書籍や算額なども「答曰く、」や「術曰く、」を含む形で書かれている。
アラビアの数学
インド数学から取り入れた特に「代数学(方程式)」が発達。インド数学とギリシア数学の東西の学問が融合された。
ヨーロッパでは紀元前のローマから中世の間の1000年以上めぼしい数学の発展はなかった。帝政のローマでは実用性のない論証的幾何学は注視されなかった。その間にアラビアで復活したうえで近世のヨーロッパに逆輸入された。
10世紀ごろにイスラム帝国にギリシア幾何学が復活。
これは教王の学問奨励で散らばっていたユークリッド原論などの資料がまとめ直されたため。後に大きな意味を持たらせる。
アル・フワリズム(9世紀)
アルゴリズムの語源(アル・フワリズムの名前)になった人。
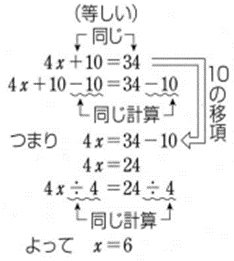
天秤を見て、方程式に「移項法」という方法を思い付き導入した。
これにより、機械的に方程式が解けるようになった。
それを「al-gebra」の本にまとめた。「gebra」が代数で「al」は英語でいう冠詞(the)
日本の数学(和算)
「日本国見在書目録」(889-897)によると少なくとも当時日本国内にあった 1579部の書物のうち数学に関係のあるものも 55部(175巻)に及んでいることがわかる。しかし、 「綴術」などが十分に消化された形跡はなく、日本人はさほど積極的に吸収はせず、そこから新しい数学を発展するなどは思いも及ばなかったようすである。
奈良時代に律令制できた式部省の下には、官吏(かんり)登用のための大学制度ができ算博士(さんはかせ)という数学専門職がもうけられていたが教育水準、地位はともに低く、世襲化し学問は育たなかった。平安末期には形骸化してしまい世襲の算博士だけ残る形となった。
それでも「九章算術」だけは、一部にもせよ、鎌倉時代、室町時代を経て江戸時代にまで読みつがれてゆき、和算勃興の1つの原動力となったようだ。
関孝和の主な業績
- 演段術の創始
- ホーナーの近似解法
- 補間法
- 方程式の判別式
- 導関数に相当する式
- 極値
- 方程式の解の変換
- 各種の級数
- ベルヌーイ数
- 正n角形の辺と対角線の関係式
- 招差法
- 整数論
- 魔方陣、円攅(円陣)
- エクストラポレーション
- 各種の曲線
- パップス・ギュルダンの方法
- 天文、暦についての多くの研究
微積分の歴史
演算記号
動画
海外
英語なので自動翻訳して見る。最後尾のは自動翻訳は出来ない。
日本
【究進塾】新井先生の数学史
N予備校
数学史(2022年度)
加藤文元先生特別講義 共通 数学史 第1回のみYouTubeで公開 https://www.nnn.ed.nico/courses/1068/chapters/18787
| No | 講義内容 | 講義時期 |
|---|---|---|
| 第1回 | 古代バビロニアの数学 | 2022年4月19日 (火) 19:00~ (94分) |
| 第2回 | 古代エジプトの数学 | 2022年5月24日 (火) 19:00~ (90分) |
| 第3回 | 記数法の歴史 | 2022年6月28日 (火) 19:00~ (92分) |
| 第4回 | 古代ギリシャ数学① | 2022年7月25日 (月) 19:00~ (94分) |
| 第5回 | 古代ギリシャ数学② | 2022年8月30日 (火) 19:00~ (90分) |
| 第6回 | 古代ギリシャ数学③ | 2022年9月27日 (火) 19:00~ (90分) |
| 第7回 | イスラムの代数学 | 2022年10月17日 (月) 19:00~ (90分) |
| 第8回 | 近代西洋数学① | 2022年11月28日 (月) 19:00~ (90分) |
| 第9回 | 近代西洋数学② | 2022年12月27日 (火) 19:00~ (90分) |
| 第10回 | 円周率の歴史 | 2023年1月24日 (火) 19:00~ (93分) |
| 第11回 | 非ユークリッド幾何学への道 | 2023年2月28日 (火) 19:00~ (95分) |
| 第12回 | 空間と構造 | 2023年3月13日 (月) 19:00~ (90分) |
幾何学の歴史(2023年度)
本講義では、幾何学の歴史を通じて、数学の世界に浸ることができます。数学の奥深さと魅力を探求する旅に出かけましょう!
幾何学の歴史 — 非ユークリッド幾何学への道 —
| No | 講義内容 | 講義時期 |
|---|---|---|
| 第1回 | 三平方の定理 | 2023年4月17日 (月) 19:00~ (93分) |
| 第2回 | 三角形の内角の和 | 2023年5月29日 (月) 19:00~ (93分) |
| 第3回 | ユークリッド 『原論』 ① | 2023年6月26日 (月) 19:00~ (93分) |
| 第4回 | ユークリッド 『原論』 ② | 2023年7月31日 (月) 19:00~ (93分) |
| 第5回 | ユークリッド 『原論』 ③ | 2023年8月28日 (月) 19:00~ (93分) |
| 第6回 | ユークリッド 『原論』 ④ | 2023年9月25日 (月) 19:00~ (93分) |
| 第7回 | サッケーリ=ルジャンドルの定理 | 2023年10月30日 (月) 19:00~ (94分) |
| 第8回 | 平行線公準証明の試み | 2023年11月27日 (月) 19:00~ (93分) |
| 第9回 | ランベルトの定理 | 2023年12月25日 (月) 19:00~ (95分) |
| 第10回 | 非ユークリッド幾何学の発見 | 2024年1月22日 (月) 19:00~ (90分) |
| 第11回 | 曲面の理論 | 2024年2月26日 (月) 19:00~ (94分) |
| 第12回 | ポアンカレ円盤モデル | 2024年3月18日 (月) 19:00~ (90分) |
ゆる数学史ラジオ
はじめて読む数学の歴史-上垣渉の本を解説
年表
| 年 | 出来事 |
|---|---|
| 前3万年 | 数の切り傷 |
| 前8000年 | カルクリの出現(メソポタミア) |
| 前3300年 | 最初の数字(シュメール, エラム) 最初の記数法 |
| 前2700年 | 楔形数字 |
| 前2000年 | 10進法の出現 |
| 前1800年 | 最古の位取り記数法(バビロニア) |
| 前1300年 | 中国数字の出現 |
| 前6世紀 | 通約不能量の発見(ピタゴラス学派) |
| 前4世紀 | 無限の概念の危機(アリストテレス) |
| 前300年 | ギリシア式アルファベット記数法 |
| 前3世紀 | ゼロの出現(バビロニア式記数法のゼロ) 極限の概念(アルキメデス) |
| 前2世紀 | 中国式位取り記数法 インド数字のもととなる9つのブラフミー数字の出現 |
| 後1世紀 | 負の数 |
| 4~5世紀 | インド式位取り記数法 ゼロをともなう10進記数法(インド) |
| 5~9世紀 | マヤ式位取り記数法 |
| 8世紀末 | インド式算術、バグダッドに伝来 |
| 9世紀初 | アル・フワーリズミーの算術書 |
| 10世紀 | ゴバール数字(北アフリカとイベリア半島) |
| 12~13世紀 | インド式算術,西欧に伝来 |
| 12~15世紀 | 算用数字(いわゆるアラビア数字)の使用定着 |
| 13世紀 | 数列の使用(フィボナッチ) |
| 15~16世紀 | 印刷術により,算用数字の字体が固定化する筆算の有用性が認められる |
| 16世紀 | 連分数の体系的使用(ボンベリ) 複素数の萌芽(カルダーノ , ボンベリ) |
| 16世紀末 | 文字表記の発明(ヴィエト) |
| 1614年 | 対数表の完成(ネイピア) |
| 1635年 | 無限小値(カヴァリエリ) |
| 1637年 | 解折幾何学の誕生(デカルト) |
| 1638年 | 無限集合の萌芽(ガリレイ) |
| 1654年 | 数学的帰納法の原理(パスカル) |
| 1677年頃 | 微積分法の発見(ニュートン,ライプニッツ) 無限級数の使用(ニュートン, ライプニッツ) |
| 1797年 | 複素数の幾何学的解釈(ガウス) |
| 1820年 | 集合の濃度の萌芽(ボルツァーノ) |
| 1825年 | 累乗根で書けない代数的数の発見(アーベル) |
| 1843年 | 四元数の発明(ハミルトン) |
| 1844年 | 超越数の発見(リウヴィル) 広義量論(グラスマン) |
| 1867年 | 形式不易の原理(ハンケル) |
| 1872年 | 最初の無理数論(デデキント) |
| 1883年 | 2番目の無理数論(カントール) 超限数(カントール) |
| 1897年 | 集合論の矛盾発見(ブラリ・フォルティ) |
| 1994年 | フェルマーの定理証明(ワイルス) |
| 西洋(ヨーロッパ、アラビア) | 東洋(日本、中国、インド) | |
|---|---|---|
| 前3000頃 | メソポタミアに六十進法記数法出現 | 黄河文明(中国) インダス文明(インド) |
| 前1500頃 | 殷王朝成立(中国) | |
| 前1100頃 | 九章算術の基となるものの存在を確認(中国) | |
| 前2000頃 | 古代バビロニアにて円周率の近似 正六角形の周と円周との比較により円周率の近似値として3,$\frac{22}{7}\fallingdotseq3.142857$, $\frac{25}{8}=3.125$が使われていた。 | |
| 前1650頃 | アーメス・パピスルス(エジプトの数学書) 分数計算、土地の面積、倉庫の容積など。円と面積がほぼ等しい正方形から円周率の近似値として $\frac{256}{81}\fallingdotseq3.1065$ | |
| 前600頃 | ターレス(ギリシャ) 数学の父、ギリシャ哲学、科学の発端 | |
| 前540頃 | ピタゴラス(ギリシャ) 三平方の定理 | |
| 前479 | 孔子没(中国) | |
| 前450頃 | エレア派のゼノン(ギリシャ) 質疑応答により知識を探求する方法(弁証法) | |
| 前330頃 | ユークリッド(ギリシャ) 『原論』成立 | |
| 前221頃 | 秦の始皇帝天下統一(中国) | |
| 前200頃 | アルキメデス(ギリシャ) 浮力の計算。円の直径と円周, 円の半径の2乗と円の面積が同じ比であることを証明。円に外接、内接するそれぞれの正 $3 \times 2^n$角形の辺の長さを$p_n,q_n$としたときに成り立つ、漸化式 $\frac{2}{p_{n+1}}=\frac{1}{p_n}+\frac{1}{q_n}$を証明し $\frac{223}{71} < \pi < \frac{22}{7}$, 小数で表すと$3.14084 < \pi < 3.14286$ を求めた。 | |
| 前200頃 | エラトステネス(ギリシャ) 素数の発見法『エラトステネスの篩』 地球の大きさ | |
| 前200頃 | ヘロン(ギリシャ) 三角形の面積公式(ヘロンの公式) 発明家 | |
| 57 | 倭奴国(日本)後漢に朝貢(中国と公式交渉開幕) | |
| 100頃 | メネラウス(ギリシャ) 共線定理(メネラウスの定理) | 張衡(後漢太史令) (中国) 円に外接する正方形の周と円周を比べ、円周率を√10≒3.162とした。 |
| 150頃 | プトレマイオス(英称 トレミー)(ギリシャ) 球面三角法 天動説 円周率の近似を 377/120≒3.1417とする。 | 『九章算術』完成(その後も注釈は追加していく)(中国) |
| 250頃 | ディオファントス(ギリシャ) 代数学の父と呼ばれ16世紀以降のヨーロッパにおける代数学発展にも深く影響 | |
| 260頃 | 劉徽『九章算術』に注解を付す(中国) 正3072角形を用いて円周率を3.1416 を求めた |
|
| 480頃 | 祖沖之『綴術』(中国) 古代中国数学の最高水準を示す書物だったと思われるが現存していないため、詳しい内容は分からないが円周率の近似分数して約率 22/7, 密率 355/113 を出していた。後者は西洋ではずっと後代になるまで知られていない。 |
|
| 500頃 | アリヤバータ(インド) 円周率の近似値を 3.1416 とした 地動説、惑星の楕円軌道 |
|
| 538 | 仏教伝来(日本) | |
| 607-894 | 遣隋使、遣唐使派遣(日本) 日本へ中国数学が移入される。しかし、『綴術』などが十分に消化された形跡はなく、日本人はさほど積極的に吸収はせず、そこから新しい数学を発展するなどは思いも及ばなかったようすである。それでも『九章算術』だけは一部にもせよ、鎌倉時代、室町時代を経て江戸時代にまで読みつがれてゆき、和算勃興の1つの原動力となった。 |
|
| 628 | ブラーフマグプタ(インド) 算術書『ブラーマ・スプタ・シッダーンタ』を著し、そこで 0 と負の数に触れた。また、正12,24,48,96角形の周の長さから、n が大きくなるにつれ正$3 \times 2^n$角形の周の長さは$\sqrt{10}$に近づくとし、これを円周率とした。 |
|
| 659 | 『算経十書』成立(中国) 『九章算術』『綴術』のほか8つの算術書と合わせこう呼ばれるようになる。 唐時代に官学の教科書として使われ、日本にも渡っていた。 |
|
| 830頃 | アル・フワーリズミー(ペルシャ) 四則演算、代数方程式の解法、二次方程式、幾何学、三角法、数の十進法表記で「0」ゼロを空いている桁に使用 | |
| 1100頃 | ウマル ! ハイヤーム(ペルシャ) 放物線と円のあいだの交点によって三次方程式を解く方法を考案 | |
| 1200頃 | ピサのレオナルド(フィボナッチ)(イタリア) 『算盤の書』の出版を通じてアラビア数字のシステムをヨーロッパに導入した。正96角形を用いて円周率を$\frac{864}{275}\fallingdotseq3.1418$を求めた。 | |
| 1247 | 秦九韶(中国) 『天元術』開拓。算木を用いた器具代数により中国数学は一段の飛躍を遂げる |
|
| 1299 | 朱世傑(中国) 『算学啓蒙』を著した。この数学的内容は、初等算術から始まり、線形連立方程式や1変数の代数方程式(2次,3次,4次,5次)に至る。しかし、代数方程式の立式に多項式の四則演算を利用する天元術が『算学啓蒙』によって初めて日本に紹介されたので、日本数学史では最も重要な資料である。この書によって、建部賢弘と彼の師である関孝和は天元術を習得した。 |
|
| 1400頃 | マータヴァ(インド) 無限級数 $\dfrac{\pi}{4}=\sum_{n=0}^{\infty}\frac{-1}{2n+1}=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}-\cdots$ を得る。これはのちにライプニッツの公式と呼ばれるようになった。 |
|
| 1545 | タルタルリア(イタリア) 3次方程式 弾道計算 | |
| 1545 | カルダノ(イタリア) 『偉大なる術』にて3次方程式の解法。三次方程式の解を示す際に世界ではじめて虚数の概念を導入した。 | |
| 1548 | フェラーリ(イタリア) 4次方程式の解法。カルダノの弟子。 | |
| 1583 | ガリレイ(イタリア) 振り子の等時性 | |
| 1592 | 程大位『算法統宗』(中国) 当時普及したそろばんの使用法と日常必要な諸算法を説き、多くの版を重ねた。日本に伝えられて初期の和算家に学ばれ、特に本書を底本とした吉田光由の《塵劫(じんこう)記》(1627年)を通じて和算の発展に大きな影響を与えた。 |
|
| 1594 | ネイピア(スコットランド) 対数の発見。対数表の作成。 | |
| 1609,1619 | ケプラー(ドイツ) 惑星の運動に関する法則 | |
| 1610 | ルドルフ・ファン・コイレン(ドイツ) 正32212254720角形の辺の長さを計算し、35桁目までπの正しい値を計算した。 | |
| 1622 | 毛利重能(日本) 現在知られている中では最も古い和算家。著書『割算書』は、江戸時代初期を代表する貴重な和算書である。後の代表的な和算家吉田光由や今村知商、あるいは関孝和の師匠でもあった高原吉種などの弟子達を育てた。 |
|
| 1627 | 吉田光由『塵劫記』(日本) 『算法統宗』からヒントを得て『塵劫記』を執筆した。数の桁の名称や単位、掛け算九九などの基礎的な知識のほか、面積の求め方などの算術を日常生活に身近な話題をもとに解説しており、一冊で当時の生活に必要な算術全般をほぼ網羅できるような内容となっている。江戸時代に出版された数学書のベストセラーかつロングセラーとなった。江戸時代の多くの和算家にも影響を与え、後に和算の大家となった関孝和も若いころ『塵劫記』を用いて数学を身につけていった。 |
|
| 1637 | デカルト(フランス) 解析幾何学 | |
| 1639 | 今村知商『竪亥録』(日本) 測量や求積に関係する公式集。漢文で専門家向けに書かれた。弓型の孤と弦の関係に関する近似公式が見られる。 |
|
| 1654 | フェルマー(フランス) 確率論、数数論 | |
| 1661 | 礒村吉徳『算法闕疑抄』(日本) 『塵劫記』以来発達してきた数学は本書にすべてまとめられ、代数方程式を使わないで珠算でできる最高度の数学が集大成されている。 |
|
| 1663 | 村松茂清『算俎』(日本) 円に内接する正$2^n$角形(2<n<15)の辺の長さから小数点以下7桁まで正しい円周率を和算家として、はじめて数学的な方法で求める。 |
|
| 1666 | ニュートン(イギリス) 微分積分学 万有引力の法則 1687年、プリンピキア出版 | |
| 1673 | 村瀬義益『算法勿憚改』(日本) | |
| 1683 | 関孝和『三部抄』『七部書』(日本) | |
| 1684,1688 | ライプニッツ(ドイツ) 微分積分学 $arctan(x)=\displaystyle \sum_{n=0}^{\infty}\frac{(-1)^n}{2n+1}x^{2n+1}$(x=1とするとマターヴァと同じ式)ほぼ同時期にグレゴリー(スコットランド)も発見 | |
| 1710 | 建部賢弘『大成算経』(日本) | |
| 1722 | 建部賢弘『綴術算経』(日本) 円周率に関連した一連の研究が最も重要で、後の円理の発展の基礎になった。まず、古来からある正多角形で円を近似する方法に「累遍増約術」(Richardson補外)を適用し、円周率を41桁まで正しく求めた。 |
|
| 1724 | ベルヌーイ(スイス) 微分方程式など | |
| 1744 | 松永良弼没(日本) πなどを種々の級数の形で表わした結果を建部の結果も含めて示す。その中にはオイラーより早く得られた結果もある。 |
|
| 1752 | オイラー(スイス) 多面体定理 | |
| 1757 | 久留嶋義太没(日本) 円理、極大極小問題、整数論など。当時の西洋数学と前後を争うような結果も少なくない。 |
|
| 1798 | 安島直円没(日本) 円や球の求積法を、級数の和の形で統一的に扱う。これは現代の区分求積法に一歩近づいた。 |
|
| 1799 | ガウス(ドイツ) 代数学の基本定理ほか | |
| 1823 | コーシー(フランス) 解析学 | |
| 1829 | ロバチェフスキー(ロシア) 非ユークリッド幾何学 | |
| 1824 | アーベル(ノルウェー) 5次方程式の代数的非可解性 | |
| 1827 | ヤコービ(ドイツ) 楕円関数論 | |
| 1830 | ボリヤイ(ハンガリー) 非ユークリッド幾何学 | |
| 1830 | ガロア(フランス) 方程式論 | |
| 1832 | ワイエルシュトラス(ドイツ) 楕円関数論 | |
| 1834 | ハミルトン(スコットランド) 解析力学 | |
| 1839 | 和田寧没(日本) 和算家最後の花火といわれるほどの人物。 |
|
| 1851 | リーマン(ドイツ) アーベル関数論ほか | |
| 1872 | 学制発布 和算を廃し、西洋数学を採用 |
|