文書の過去の版を表示しています。
目次
数学史のメモ
今後、数学史をまとめていく上でメモをまとめていく。
数学セミナー編集部が著した100人の数学者一覧 + 追加分
数学史の勉強が必要か
ChatGPTに聞いてみました。
数学の歴史についての勉強は、数学の起源や発展、そして現代における役割を理解するために役立ちます。また、数学の歴史を学ぶことで、数学が社会や文化にどのように影響を与えてきたかを知ることができます。さらに、歴史上の偉大な数学者たちがどのような発明や理論を行ってきたかを学ぶことで、数学に対する興味を深めることができます。
ただし、数学の歴史を勉強する必要はありません。数学について学ぶことは、それ自体が重要であり、歴史を知ることはあくまで補助的なものです。
数学の歴史を勉強することによって、数学に対する興味を深めることができるだけでなく、数学的思考力を養うこともできます。
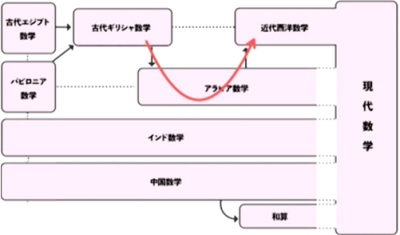
巨大な遠回り
- ヘレニズム期以後、ギリシャ世界の数学・科学・哲学の知見は西欧文化圏にはほとんど拡散しなかった。
- 5世紀〜7世紀にかけて、主にシリア文明圏に引き渡される(シリア・ヘレニズム)。イスラム教帝国によってこれらがアラビア語訳。
- 12世紀ごろから西欧に逆輸入(12世紀ルネサンス)。
- 12世紀ルネサンスでは、イスラム地域から数学書が数多くもたらされ、アラビア語からラテン語に翻訳された(大翻訳運動)。
- 12世紀ルネサンス期以後の西欧では、数学の担い手の社会的階層が広がった。
- 特に職人・商人階級を中心に計算術や代数学などの実用的な数学の需要が高まった。(アラビア数字や記法を積極的に採用)
- イタリアでは「算法教師」が計算やアルゴリズム主体の数学を発展させ、イタリアにおける代数学の基礎を築いた。
シリア・ヘレニズム
- ネストリウス派(イエス=神人両性、431年エフェソス公会議で異端宣告)のシリア亡命。時のササン朝ペルシャ皇帝に歓迎される。
- 単性論者(人としてのイエスも神性、451年カルケドン公会議で異端宣告)。シリアで細々と修道生活しながらギリシャ文献のシリア訳。
西洋独自の発達
- ルネサンス期以降:ギリシャ以来の「総合的・演繹的数学」とインド・アラビア由来の「解析的・発見的数学」
- これらを融合・統一する試み
- 幾何学の算術化
- 代数学の幾何学的な一般性と厳密性
- ヴィエトの記号代数学
- 運動の数学的記述への試み
- 不可分者の概念
- 瞬間の速度・曲線の接戦
- 微分積分学の発見=微分積分学の基本定理の発見
- 無限小算術の厳密化ではない
- 19世紀西洋数学
- 量から概念へ
人物
古代・中世の数学
アリスタルコス
アリスタルコス(BC310頃-BC230頃)は、古代ギリシアの天文学者。ギリシャのサモス島に生まれたため、同名の人物と区別するためにサモスのアリスタルコスといわれる。
宇宙の中心には地球ではなく太陽が位置しているという太陽中心説(地動説)を最初に唱えたため、古代のコペルニクスと呼ばれる。
天体三角測量
ヒッパルコス
ヒッパルコス(BC190頃-BC120頃)は、古代ギリシアの天文学者。
- 現代にすべてつながる46星座を決定した。
- 恒星を1等星から6等星までの6段階に分けた。若干形を変えたが視等級として現代でも使われている。
- 三角法による測量を行った。
天球上に緯度と経緯を導入し天文学に三角法を用いた。
平面三角法を確立し精密な三角比の数表を作成した(加法定理 $\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta$ を導き、これを用いることで、7.5°から180°までの7.5°刻みの数表を作成)
正弦(Sinus rectus)
プレイマイオス
プレイマイオス(BC83頃-BC168頃)は、数学、天文学、占星学、音楽学、光学、地理学、地図製作学など幅広い分野にわたる業績を残した古代ローマの学者。
三角関数表
ピュタゴラス
ピュタゴラス(BC570頃–BC495頃)は古代ギリシアの数学者・哲学者。
「万物は数である」と考え、数学を宗教的・哲学的に体系化した。
直角三角形の関係を示すピュタゴラスの定理で知られる。
エウドクソス
エウドクソス(BC408頃–BC355頃)は古代ギリシアの数学者・天文学者。
無理数を扱うための「尽きることのない分割法(求積法)」を考案。
微積分の先駆的思想を含んでいる。
エウクレイデス(ユークリッド)
エウクレイデス(BC300頃)は古代ギリシアの数学者。
著書『原論』で幾何学を公理体系として整理した。
2000年以上にわたり数学教育の基礎となった。
アルキメデス
アルキメデス(BC287頃–BC212頃)は古代ギリシア最大の数学者。
円周率の計算、体積・面積の研究で業績を残した。
てこの原理や浮力の法則でも知られる。
ヒュパティア
2009年スペイン映画「アレクサンドリア」の主人公である女性
西暦4世紀、キリスト教が定着し異教の排斥が行なわれ始めた時代の、女性天文学者ヒュパティアの学問に殉じた半生をアレクサンドリアを舞台に描く。
ボエティウス
学問語であるギリシャ語の識字率が急速に低下、ギリシャ時代の高度な数学・科学・哲学の知識が急速に失われ始める。ラテン語の識字率が高い状態になっている時代背景がある。
- 480年〜525年。古代ローマ末期のイタリアの哲学者・政治家・修辞学者
- ユークリッドやアリストテレスなどの著作をラテン語に翻訳しようとした。
- しかし、政治的嫌疑をかけれら、東ゴートのテオドリック王によって処刑。
アポロニオス
アポロニオス(BC262頃–BC190頃)は円錐曲線を体系化した数学者。
楕円・放物線・双曲線の理論を確立した。
後の天文学や解析幾何に大きな影響を与えた。
ディオファントス
ディオファントス(3世紀頃)はギリシアの数学者。
整数解を求める「ディオファントス方程式」を研究した。
代数学の祖と呼ばれる。
アル・フワーリズミー
アル・フワーリズミー(9世紀)はイスラム世界の数学者。
「代数(アルジャブル)」を体系化した。
彼の名から「アルゴリズム」という言葉が生まれた。
サービト・イブン・クッラ
サービト(836–901)はイスラムの数学者・天文学者。
ギリシア数学を翻訳・発展させた。
数論や幾何学に貢献した。
イブラーヒーム・イブン・シナーン
イブン・シナーン(908–946)はイスラムの数学者。
積分的手法による求積問題を研究した。
アルキメデスの研究を発展させた。
イブヌル・ハイサム
イブン・ハイサム(965–1040)は光学の父。
実験に基づく科学的方法を確立。
数学・光学・物理学に大きな影響を与えた。
ウマル・ハイヤーム
ウマル・ハイヤーム(1048–1131)は詩人・数学者。
3次方程式を幾何的に解いた。
暦の改良にも貢献した。
バースカラ
バースカラ2世(1114–1185)はインドの数学者。
微分に近い概念を扱った。
代数・三角法を発展させた。
フィボナッチ
フィボナッチ(1170頃–1250頃)はイタリアの数学者。
『算盤の書』でアラビア数字を欧州に普及。
フィボナッチ数列で有名。
ニコル・オレム
ニコル・オレム(1320頃–1382)は中世フランスの学者。
グラフ的表現を用いて数量変化を分析。
関数概念の先駆者。
マーダヴァ
マーダヴァ(14世紀)はインドの数学者。
無限級数による円周率計算を行った。
解析学の先駆的研究者。
東アジアの伝統数学
劉徽
劉徽(3世紀)は中国の数学者。
『九章算術』に詳細な注釈を付けた。
円周率の高精度計算を行った。
祖冲之
祖冲之(429–500)は中国の数学者・天文学者。
円周率を3.1415926…まで計算。
世界最高精度を達成した。
朱世傑
朱世傑(13世紀)は中国の数学者。
高次方程式を行列的に解いた。
『算学啓蒙』『四元玉鑑』を著した。
梅文鼎
梅文鼎(1633–1721)は清代の数学者。
中国数学と西洋数学を融合した。
近代化の橋渡し役。
関 孝和
関 孝和(1642–1708)は江戸時代の数学者。
日本独自の和算を発展。
行列式に近い概念を発見。
建部 賢弘
建部 賢弘(1664–1739)は和算家。
円周率を40桁以上計算。
関孝和の弟子。
和田 寧
和田寧(18世紀)は和算家。
測量・暦算に貢献。
実用数学を発展させた。
近代西洋数学の形成
カルダーノ
カルダーノ(1501–1576)はイタリアの数学者・医師。
3次・4次方程式の解法を初めて体系的に公開した。
確率論の先駆者でもある。
ヴィエト
ヴィエト(1540–1603)はフランスの数学者。
文字を使った代数学記法を導入。
現代代数の基礎を築いた。
ステヴィン
ステヴィン(1548–1620)はオランダの数学者。
小数表記を普及させた。
実用数学の発展に貢献。
ジョン・ネイピア
ジョン・ネイピア(1550–1617)はスコットランドの数学者。
対数を発明。
計算を飛躍的に簡単にした。
ガリレオ・ガリレイ
ガリレオ(1564–1642)はイタリアの科学者。
数学を自然科学に導入。
近代科学の父と呼ばれる。
ケプラー
ケプラー(1571–1630)はドイツの天文学者。
惑星運動の3法則を発見。
数学と天文学を融合。
デザルグ
デザルグ(1591–1661)はフランスの数学者。
射影幾何学を創始。
現代幾何の基礎。
デカルト
デカルト(1596–1650)はフランスの哲学者・数学者。
解析幾何学を創始。
座標による図形表現を導入。
カヴァリエリ
カヴァリエリ(1598–1647)はイタリアの数学者。
無限小による求積法を考案。
積分学の前身。
フェルマー
フェルマー(1607–1665)はフランスの数学者。
数論の父。
フェルマーの最終定理で有名。
トリチェッリ
トリチェッリ(1608–1647)はイタリアの数学者。
無限級数と積分研究。
気圧計を発明。
ウォリス
ウォリス(1616–1703)はイギリスの数学者。
無限積・解析学を発展。
円周率研究で有名。
パスカル
パスカル(1623–1662)はフランスの数学者。
確率論を創始。
計算機も発明。
ホイヘンス
ホイヘンス(1629–1695)はオランダの数学者。
確率論・振り子研究。
力学に貢献。
ニュートン
ニュートン(1643–1727)はイギリスの数学者。
微積分学・力学を創始。
近代物理の基礎。
ライプニッツ
ライプニッツ(1646–1716)はドイツの数学者。
微積分記号を確立。
論理学にも貢献。
ベルヌリ・ヤーコプ
ベルヌリ・ヤーコプ(1655–1705)はスイスの数学者。
確率論を発展。
大数の法則を証明。
ベルヌリ・ヨーハン
ベルヌリ・ヨーハン(1667–1748)はスイスの数学者。
解析学を発展。
オイラーの師。
マクローリン
マクローリン(1698–1746)はスコットランドの数学者。
テイラー展開の特殊形を研究。
オイラー
オイラー(1707–1783)はスイスの数学者。
解析・記号法を確立。
史上最多の業績。
ダランベール
ダランベール(1717–1783)はフランスの数学者。
偏微分方程式を研究。
ラグランジュ
ラグランジュ(1736–1813)はイタリアの数学者。
解析力学を体系化。
モンジュ
モンジュ(1746–1818)はフランスの数学者。
画法幾何学を創始。
ラプラス
ラプラス(1749–1827)はフランスの数学者。
確率論・天体力学を発展。
ルジャンドル
ルジャンドル(1752–1833)はフランスの数学者。
楕円積分・数論研究。
近代数学の展開
フーリエ
ガウス
「数学の王子」。
数論・解析・統計など多分野に貢献。
ボルツァーノ
コーシー
バベッジ
ロバチェフスキイ
アーベル
ボヤイ(ヤーノシュ)
ヤコビ
ディリクレ
ハミルトン
リューヴィル
ガロワ
群論の創始者。
方程式論を革新。
ワイエルシュトラス
ケイリー
エルミート
クロネッカー
リーマン
幾何学を拡張。
相対性理論の基礎。
デデキント
ジョルダン
リー
カントル
集合論の創始者。
無限の理論を構築。
フレーゲ
クライン
コワレフスカヤ
ポアンカレ
現代数学の開花
ヒルベルト
20世紀数学を主導。
ヒルベルトの23問題。
アダマール
ハウスドルフ
カルタン
ボレル
ラッセル
カラテオドリ
高木 貞治
ルベーグ
アインシュタイン
ブラウワー
ネーター
ヴァイル
ラーマーヌジャン
ベルナイス
バナッハ
ウィーナー
アルティン
岡 潔
コルモゴロフ
フォン・ノイマン
ゲーデル
不完全性定理を証明。
形式主義に衝撃。
ヴェイユ
ポントリャーギン
シュヴァレー
チューリング
計算理論の父。
現代コンピュータの基礎。
シュヴァルツ
用語/語源
second
ラテン語 secunda(minuta)・・・2番目の(60分の1)という意味が由来。1時間の60分の1は分、その60分の1は秒であるということ。
法則
ジャネーの法則
ジャネーの法則とは、フランスの哲学者ポール・アレクサンドル・ジャネ(1823-1899)が人間の時間の感じ方を考察し、「人間にとって現在という感じ方は、これまで生きてきた時間との比として感じている」とした。
- 10歳のときの一年は、全人生の1/10
- 30歳のときの一年は、全人生の1/30
- 60歳のときの一年は、全人生の1/60
と、このように年を取るごとに人間が体感する一年は相対的に短くなります。
「新鮮な経験」が多いほど、時間の経過は長く感じるという考え方もある。
http://visnet.ne.jp/ep/chieikasu/column/column232.html
度量衡
メートルの誕生
フランス革命の時代、ヨーロッパにはなんと40万種類もの長さの単位があったといわれている。これをみかねたフランスが国家の威信をかけて取り組んだのが「子午線測量プロジェクト」です。
世界統一単位を夢見たフランスはこの事業を成功させ「メートル」が誕生しました。
その他
定住の歴史
大航海時代
暗黒の中世からルネッサンスへ人びとの目も海外へ11〜13世紀頃、ヨーロッパではカトリック教会が大きな権威を持っており人びとの生活の中心には、キリスト教への絶対的信仰があった。この頃、イスラム勢力の支配下にあったキリスト教の聖地エルサレムを奪還しようとたびたび十字軍が組織され、キリスト教徒の騎士たちは東方への攻め込んだ。この戦いで、科学的に進んでいたイスラム文化と接するうちに、やがて頑迷なキリスト教徒たちの間にも、自己反省がおこなわれはじめる。
一方で、14世紀ヨーロッパにおいて流行したペストの影響も少なからずあった。この疫病により、ヨーロッパは人口の4分の1から3分の1を失ったという。 このため、労働力が急激に減少し、賃金が上昇。農民が流動的になることで農奴に依存する荘園制が崩壊。また人材不足は、それまで大きく超えることがなかった身分の枠を飛び越えた人材登用を促した。こうして、封建的身分制度は実質的解体へと向かったのである。これかの背景に、教会の権威の失墜がある。ペストの脅威から人びとを救えなかった宗教に代わるものとして、14〜16世紀のヨーロッパには、知識を重んじるルネサンスの時代が来る。羅針盤に航海術も発展し、世界への乗り出す大航海時代がはじまったのである。
「航海王子」と称されるポルトガルのエンリケ王子の指揮により、1422年以降アフリカ西岸を南に下る艦隊を多数派遣されたことが、大航海時代のはじまりといわれている。それまで通用していたプレイマイオス世界図では、アフリカの陸続きにアジアがあるとされ、アフリカとアジアは南半球でつながっているものと考えられていた。しかし、十字軍によって得たアラビアの知識では、アフリカには南端があり、それを超えてインドへの航海することが可能とされていた。彼らは、アフリカの先にどんな夢を見たのでだろう。1487年には喜望峰が発見され、1498年にはバスコ・ダ・ガマがカリカットに到着、インドへの直通航路が開かれた。